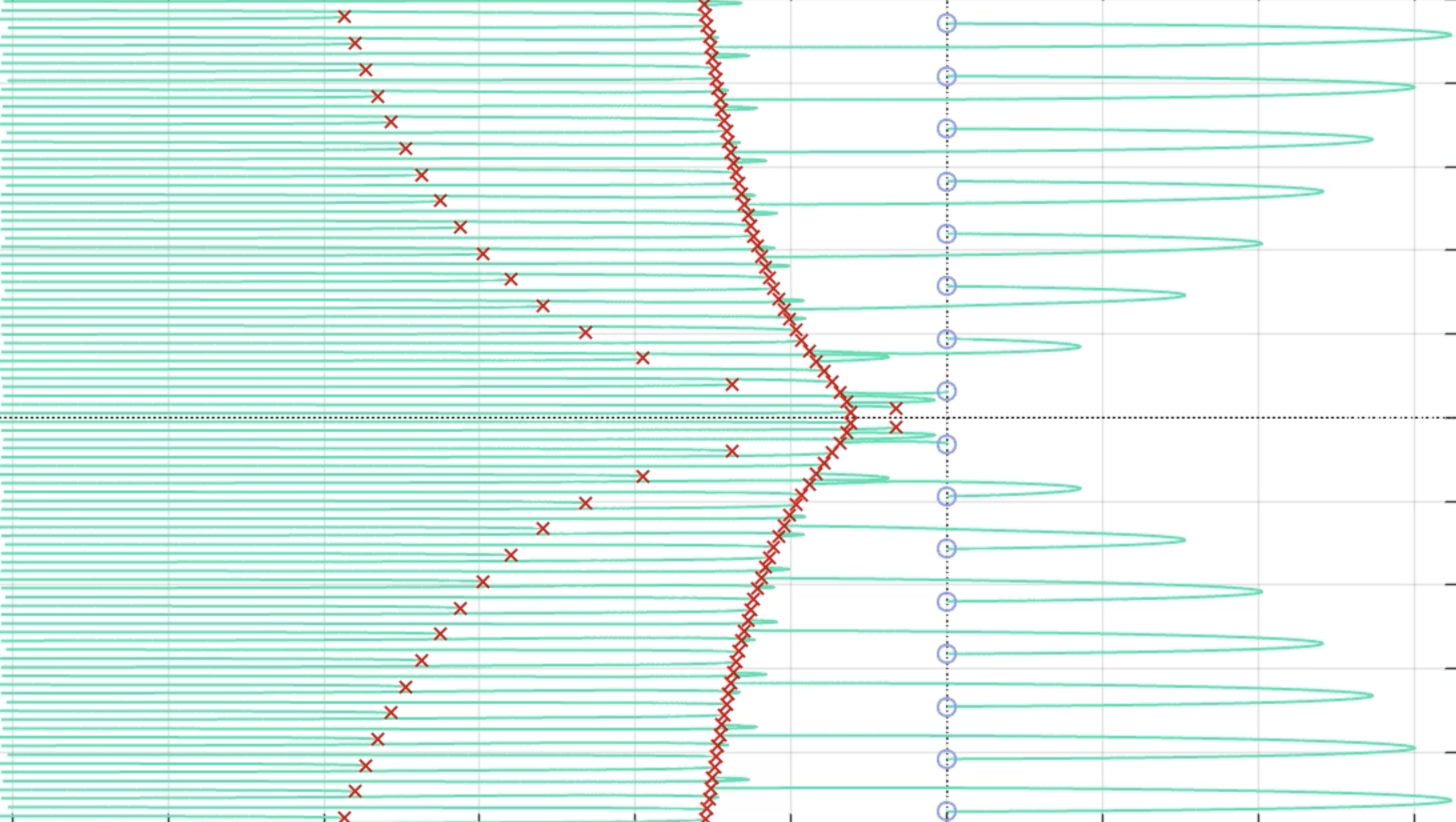
System with multiple delays
This example shows how the tdrlocus tool handles complicated systems with multiple delays. The example transfer function is
\[ H(s) = \frac{1+e^{-s}}{(1+s+e^{-2s})(5+s+e^{-5s})} = \frac{1+e^{-s}}{s^2+6s+5+(s+5)e^{-2s}+(s+1)e^{-5s}+e^{-7s}}\]
The function can be either called using string notation
reg = [-10, 5, 0, 50];
num = "1+exp(-s)";
den = "(1+s+exp(-2*s))*(5+s+exp(-5*s))";
tdrlocus(reg, num, den);
reg = [-10, 5, 0, 50];
numP = [1; 1]; numD = [0; 1];
denP = [1, 6, 5; 0, 1, 5; 0, 1, 1; 0, 0, 1]; denD = [0; 2; 5; 7];
tdrlocus(reg, numP, numD, denP, denD);
It is possible to substitute delay terms parametrically, such system can be call as
reg = [-10, 5, 0, 50];
num = "1+exp(-K1*s)";
den = "(1+s+exp(-K2*s))*(5+s+exp(-K3*s))";
tdrlocus(reg, num, den);